
Hi! This is Frank Ong. My interests lie in data science, signal processing, and imaging. I am currently a machine learning engineer at Roblox, working on recommendation systems.
From 2019 to 2020, I was a research associate at Stanford with Shreyas Vasanawala and John Pauly. There, I developed and deployed low rank matrix factorization based reconstruction methods on MRI scanners.
I did my undergrad (2013) and PhD (2018) at UC Berkeley, where I had the pleasure to work with Miki Lustig for many many years. In my Berkeley days, I also collaborated with Kannan Ramchandran on sparse FFT algorithms. And I did a wonderful summer internship with Peyman Milanfar at Google in 2017.
Please see below for an overview of my research projects!
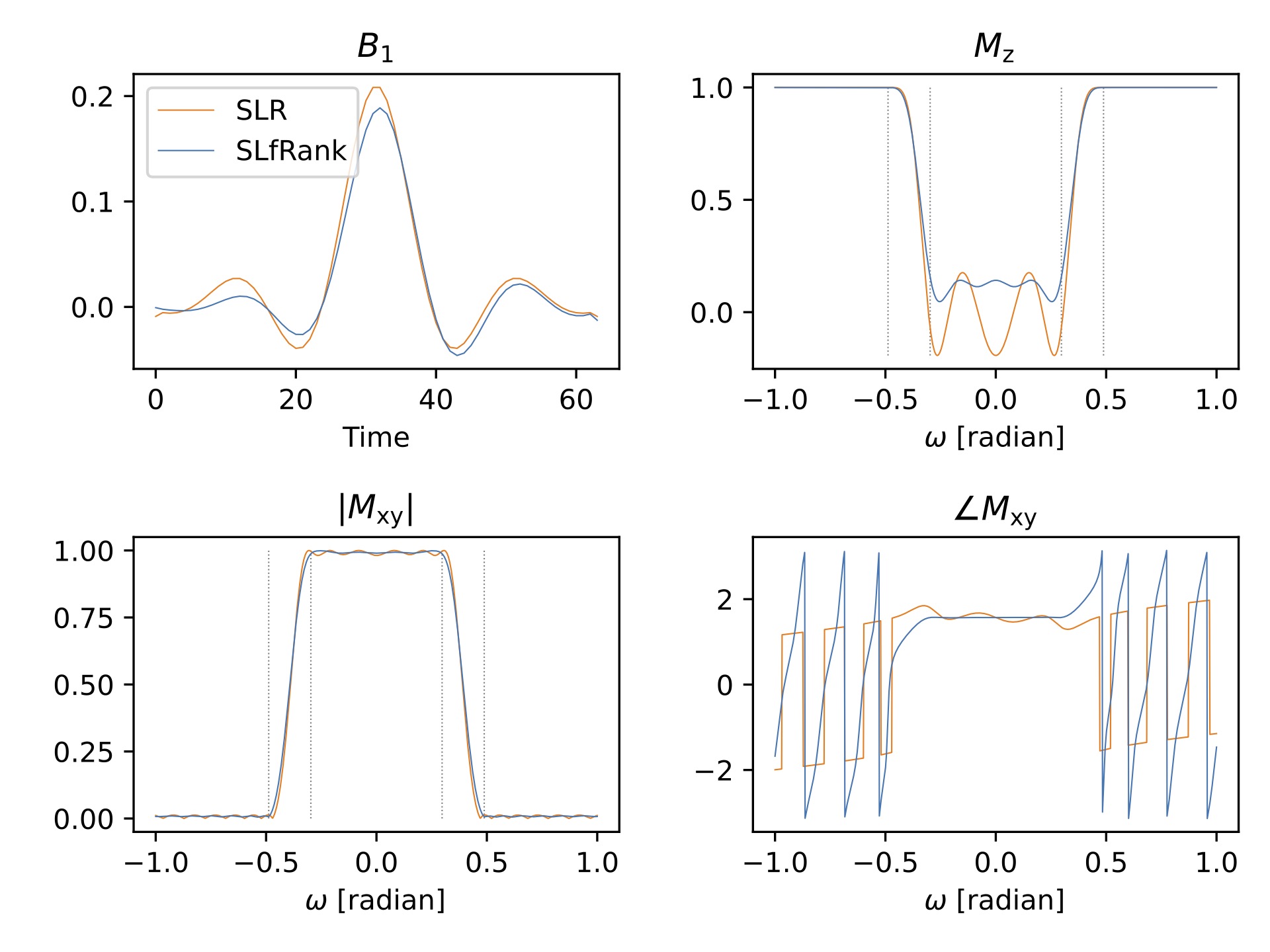
SLfRank: Improved SLR Pulse Design with Rank Factorization
with Zheng Zhong, Congyu Liao, Michael Lustig, Shreyas Vasanawala, and John Pauly
Extreme MRI: Large-scale Dynamic MRI from Continuous Acquisitions
with Xucheng Zhu, Joseph Cheng, Kevin Johnson, Peder Larson, Shreyas Vasanawala, and Miki Lustig
This project develops a framework to reconstruct large-scale volumetric dynamic MRI from rapid continuous and non-gated acquisitions. The problem considered here requires recovering ~100GBs of data from a few GBs of measurements. We propose two innovations: (1) A compressed representation using multi-scale low rank matrix factorization. (2) Stochastic optimization to reduce computation. We demonstrate the feasibility of the proposed method on DCE and pulmonary imaging.
SigPy: A Python Package for High Performance Signal Reconstruction
with Chris Sandino, Sri Koundinyan, Ke Wang, and Miki Lustig
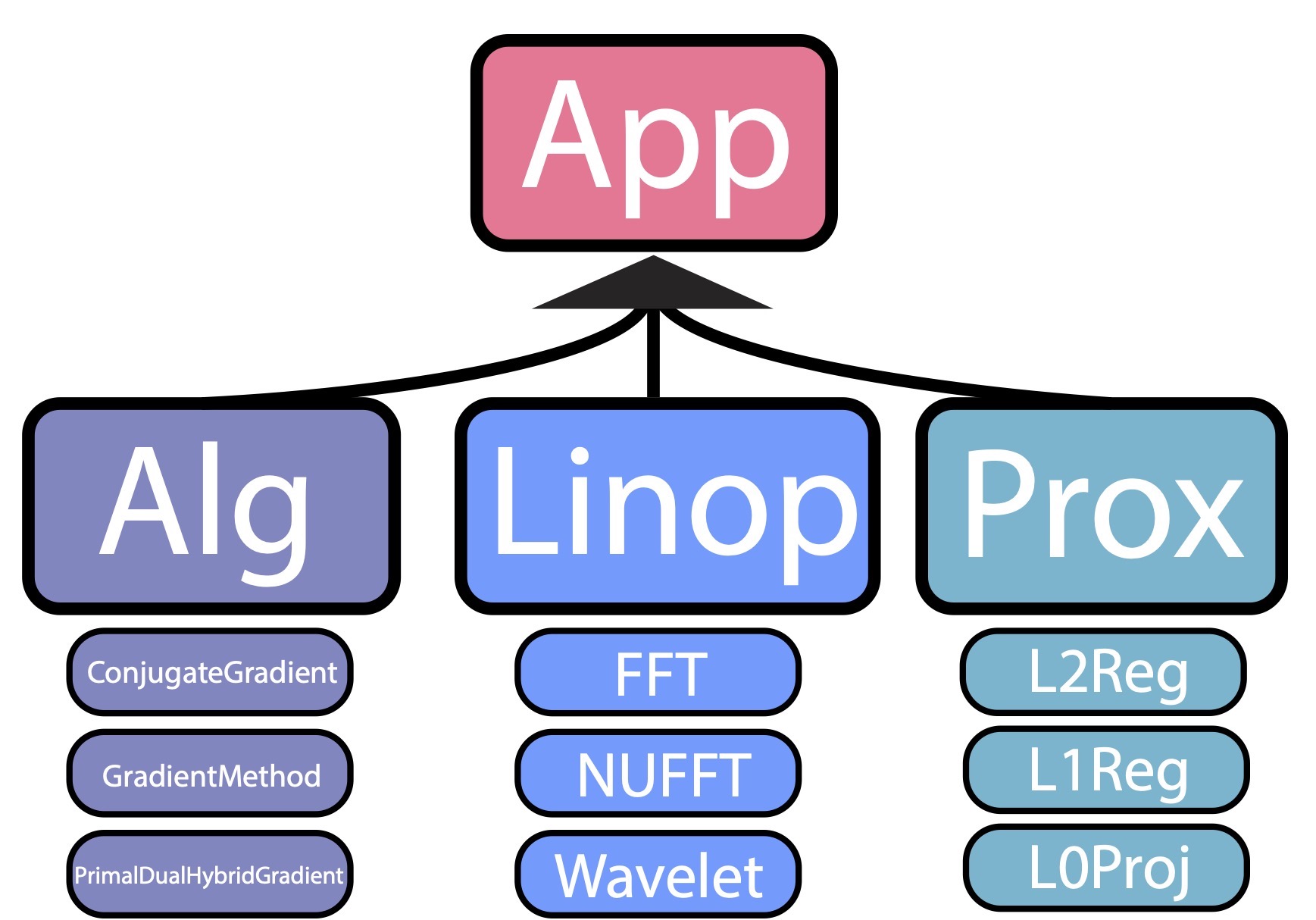
SigPy is a Python package for signal processing, with emphasis on iterative methods. It is built to operate directly on NumPy arrays on CPU and CuPy arrays on GPU. SigPy provides several domain-specific submodules: sigpy.plot for multi-dimensional array plotting, sigpy.mri for MRI iterative reconstruction, and sigpy.learn for machine learning.
k-space Preconditioning: Accelerating Non-Cartesian MRI Reconstruction without Compromises
with Martin Uecker, and Miki Lustig
We propose a k-space preconditioning formulation for accelerating the convergence of iterative MRI reconstructions from non-uniformly sampled data. Existing methods either use sampling density compensations which sacrifice reconstruction accuracy, or circulant preconditioners which increase per-iteration computation. Our approach overcomes both shortcomings. Concretely, we show that viewing the reconstruction problem in the convex dual formulation allows us to precondition in k-space using density-compensation-like operations.
Approximating Proximal Operators with Kernel Methods
with Peyman Milanfar, and Pascal Getreuer
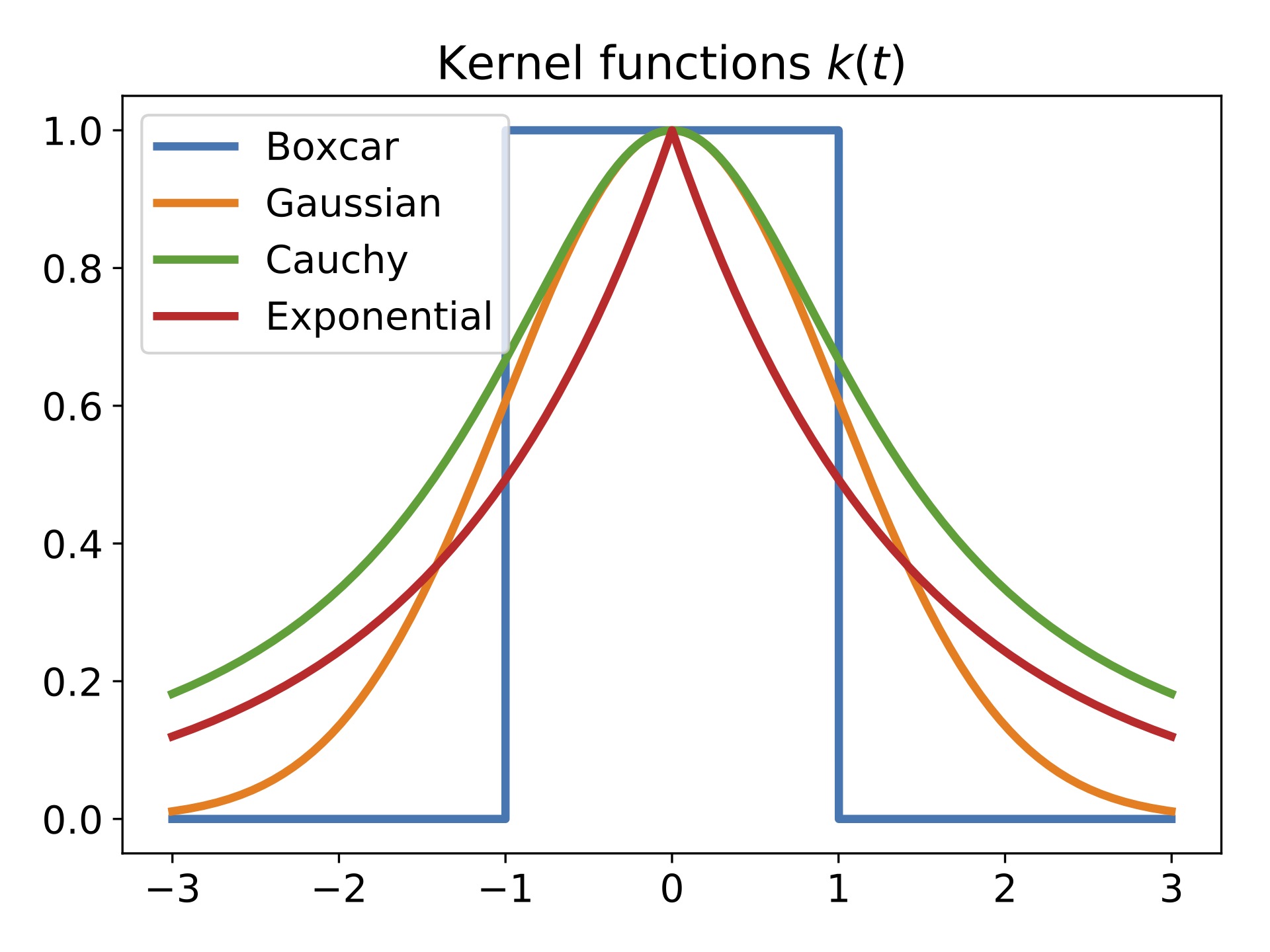
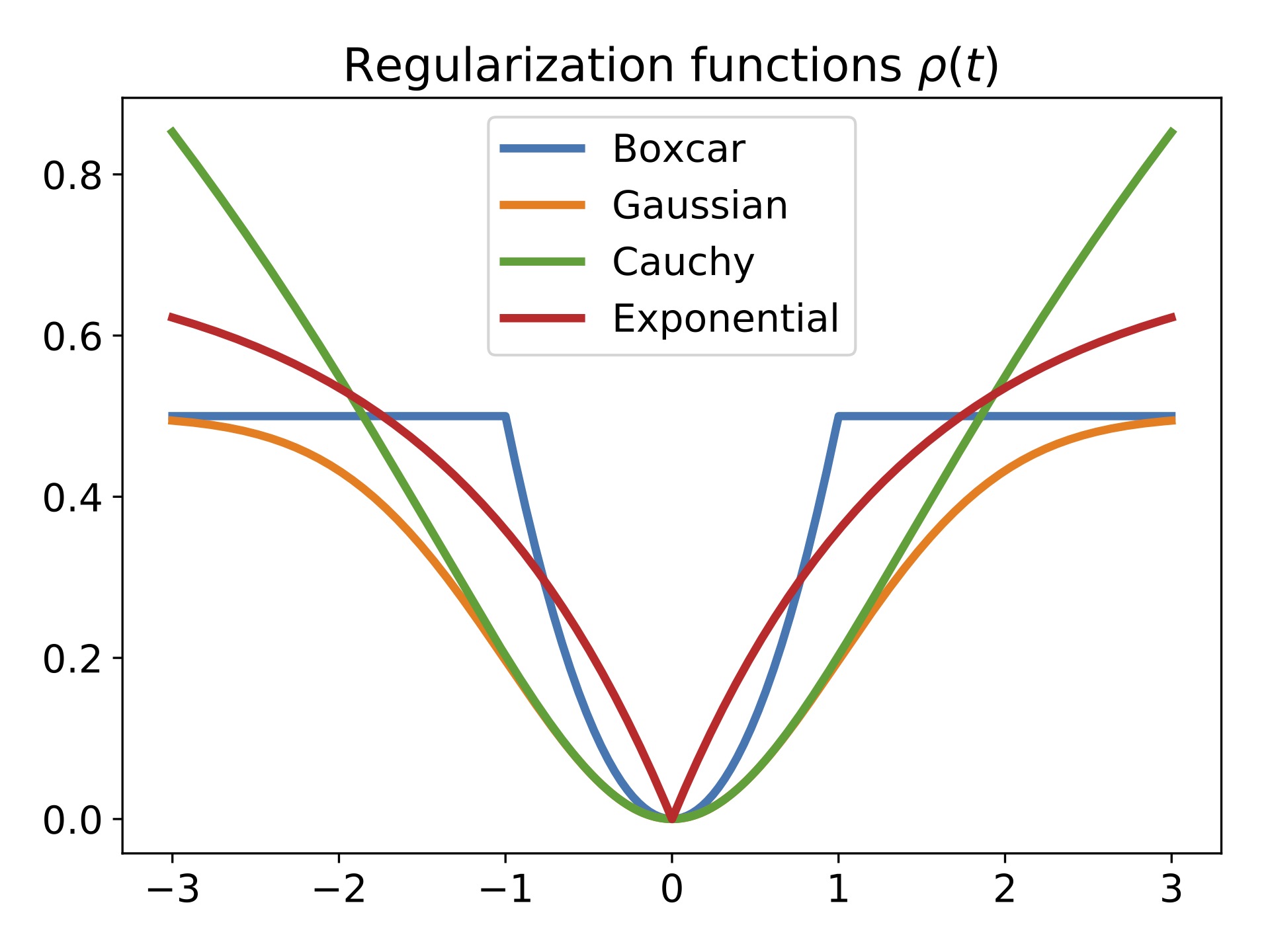
In this work, we broadly connect kernel-based filtering with general variational formulations of Bayesian regularized least squares. Our main contribution here is to establish how one can approximate the solution of the regularized least squares with use of locally adaptive filters with specific kernels.
Phase Regularized MRI Reconstruction with Phase Cycling
with Joseph Cheng, and Miki Lustig
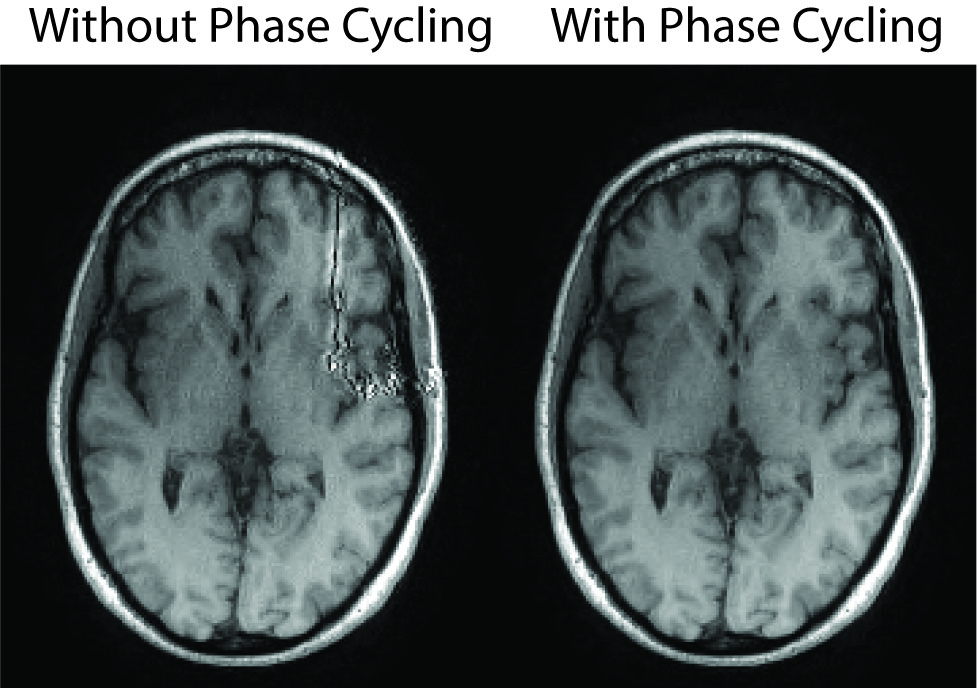
We study the problem of enforcing phase constraints in reconstruction under a regularized inverse problem framework. We propose a general phase regularized reconstruction algorithm to enable various joint reconstruction of partial Fourier imaging, water-fat imaging and flow imaging. Since phase regularized reconstruction is inherently non-convex and sensitive to phase wraps in the initial solution, we develop a reconstruction technique, named phase cycling, to render the overall algorithm invariant to phase wraps.
Multiscale Low Rank Matrix Decomposition
with Miki Lustig
We present a natural generalization of the low rank + sparse matrix decomposition and consider the decomposition of matrices into components of multiple scales. Concretely, we propose a multi-scale low rank modeling that represents a data matrix as a sum of block-wise low rank matrices with increasing scales of block sizes. We then consider the inverse problem of decomposing the data matrix into its multi-scale low rank components and approach the problem via a convex formulation. We provide theoretical recovery guarantees and practical applications.
mridata.org: An Open Platform for Sharing MRI Raw Datasets
with Gaby Nahum, Shahab Amin, Shreyas Vasanawala, and Miki Lustig
mridata.org is an open platform for researchers to share MRI raw k-space datasets. This web site provides open datasets to researchers who desire to contribute to a community of reproducible research, where they can test and validate their algorithms against known undersampled acquisitions.
BART: Toolbox for Computational MRI
with Martin Uecker (main developer), Jon Tamir, Miki Lustig and others

The Berkeley Advanced Reconstruction Toolbox (BART) is a free and open-source image-reconstruction framework for computational MRI developed by the research groups of Martin Uecker and Michael Lustig. I was an active developer for many years til 2017. BART provides common operations on multi-dimensional arrays, Fourier and wavelet transforms, as well as generic implementations of iterative optimization algorithms.
2D Sparse Fast Fourier Transform with Sparse Graph Codes
with Samir Pawar, and Kannan Ramchandran
We present a algorithm, named the 2D-FFAST, to compute a sparse 2D-DFT featuring both low sample complexity and low computational complexity. The proposed algorithm is based on mixed concepts from signal processing (sub-sampling and aliasing), coding theory (sparse-graph codes) and number theory (Chinese-remainder-theorem). Concretely, the 2D-FFAST algorithm computes a \(k\)-sparse 2D-DFT, with a uniformly random support, of size \(N = N_x \times N_y\) using \(O(k)\) noiseless spatial-domain measurements in \(O(k \log k)\) computational time.
Robust 4D Flow Denoising with Divergence-Free Wavelet Transform
with Martin Uecker, Umar Tariq, Albert Hsiao, Marc Alley, Shreyas Vasanawala, and Miki Lustig
We investigate 4D flow denoising using the divergence-free wavelet (DFW) transform. DFW is a vector-wavelet that provides a sparse representation of flow in a generally divergence-free field. It can be used to enforce “soft” divergence-free conditions when discretization and partial voluming result in numerical nondivergence-free components. Efficient denoising is achieved by appropriate shrinkage of divergence-free waveletand non-divergence-free coefficients.